Eggland’s Best provided us with the information, coupons and Visa gift card for this post about Roasted Vegetable Frittata Recipe and Giveaway. For Easter, I usually do an Egg souffle or overnight casserole dish. It is easy because you do everything before hand and the hardest part is getting home from church and getting the oven preheated and waiting the 60 minutes for it to cook. A frittata is a quicker way to but breakfast or dinner on the table. What I really like about this frittata recipe is that you can roast the veggies ahead for an even easier turn around time. We hope you enjoy this step by step on How To Make a Frittata but be sure to read further as there are sweepstakes and a giveaway below.

This roasted vegetable frittata recipe is adapted from Barefoot Contessa and chuck full of veggies and cheeses.

If you are looking to make this recipe ahead of time, you can start by roasting the veggies and then heating them up before you prepare the eggs. The best part of this recipe is that you can change out the veggies for the ones your family will enjoy.



Wow, this is a wonderful concept, not sure why mom would flip her omelets all the time when we were younger. I just remember standing far away in fear they were going to slide off the plate she was flipping them on. Kudos to mom, I don’t think one ever dropped (that we saw!!)

Once you learn how to make a frittata recipe, you will realize just how easy they are to make. Just add everything and plop it into the oven to do all the work. Not sure how I could have really messed this recipe up.

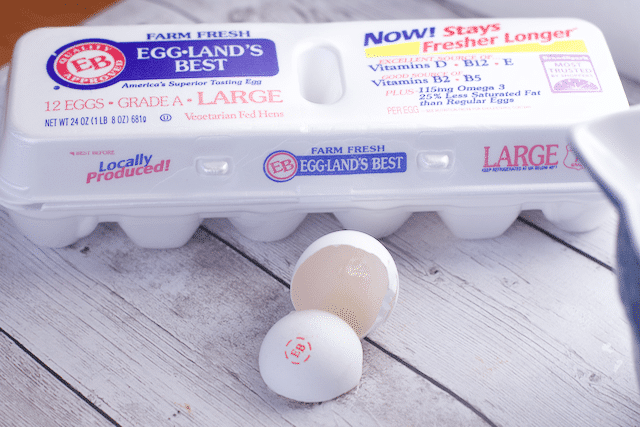
Why we like using Egglands Best Eggs!
Compared to ordinary eggs, Eggland’s Best eggs contain five times more vitamin D, 25 percent less saturated fat, more than double the Omega-3s, ten times more vitamin E, and three times more vitamin B12. Eggland’s Best’s superior nutrition is due to its proprietary all-vegetarian hen feed that contains healthy grains, canola oil and a wholesome supplement of rice bran, alfalfa, sea kelp and Vitamin E. In addition, independent testing has revealed that Eggland’s Best eggs have stronger shells than ordinary eggs, which leads to less breakage and helps them stay fresher longer than ordinary eggs

Roasted Vegetable Frittata Recipe

Roasted Vegetable Frittata Recipe
Roasted Vegetable Frittata Recipe is an easy way to make an omelet
Ingredients
- 1 small zucchini, 1-inch-diced
- 2 bell peppers, seeded and 1 1/2-inch-diced
- 1 red onion, 1 1/2-inch diced
- 1/4 cup good olive oil
- Kosher salt and freshly ground pepper
- 2 teaspoons minced garlic, 2 cloves
- 12 large Egglands Best eggs
- 1 cup milk
- 1/4 cup freshly grated Parmesan cheese
- 1 tablespoon unsalted butter
- 1/3 cup chopped scallions, white and green parts (3 scallions)
- 1/2 cup grated Gruyere cheese or cheddar if you prefer a milder cheese
Instructions
- Preheat the oven to 425 degrees.
- Place the zucchini, peppers, and onion on a sheet pan. Drizzle with the olive oil, sprinkle with 3/4 teaspoon salt and 1/2 teaspoon pepper, and toss well. Bake for 15 minutes. Add the garlic, toss again, and bake for another 15 minutes. Remove from the oven and turn the oven to 350 degrees. (this can be done ahead of time, even a few days in advance) Just reheat before next step.
- For the Egg Mixture, in a large bowl, whisk together the eggs, half-and-half, Parmesan, scant 1/2 teaspoon salt and 1/2 teaspoon pepper.
- In a 10-inch ovenproof saute' pan, melt the butter and saute' the scallions over medium-low heat for 3 minutes. Add the roasted vegetables to the pan and toss with the scallions. Pour the egg mixture over the vegetables and cook for 2 minutes over medium-low heat without stirring. Transfer the pan to the oven and bake the frittata for 20 to 30 minutes, until puffed and set in the middle. Sprinkle with the Gruyere and bake for another 3 minutes, until the cheese is just melted. Cut into 8 wedges and serve hot. Fed our family of 5 easily with 2 slices left
Nutrition Information
Yield 6Amount Per Serving Calories 338Saturated Fat 8gCholesterol 352mgSodium 249mgCarbohydrates 8gFiber 1gSugar 5gProtein 18g
EGGLANDS BEST SWEEPSTAKES:
Get creative in the kitchen and enter the 2017 Eggland’s Best Foodtography Contest. Entries will be accepted now through April 12, 2017. One grand prize winner will have a chance at $5,000 and a year’s supply of Eggland’s Best eggs! All dish creations must include at least two whole Eggland’s Best eggs.
Close to Home $25 GIVEAWAY::
One Reader (U.S. only) can win a $25 Visa gift card and one (1) coupon, valid for a free carton of Eggland’s Best eggs, so you can create delicious and nutritious recipes using the best quality ingredients, including Eggland’s Best eggs! Enter the Rafflecopter below.


I would make a bacon omelet.
I would love to make a breakfast casserole!
I would make German pancakes
That looks and sounds so good. I think I would switch up the classic deviled egg recipe and make some avocado deviled eggs topped with fresh bacon bits!
I would make a bacon and cheese quiche.
I would make french toast.
We will be boiling Easter Eggs, lots of Easter eggs
I will make an egg pie!Yummy!
I would have eggs for breakfast and then bake with them and make some great pies
Love to make Indian Egg Curry
I would make crepes!
I would be trying this frittata recipe above but I’d be adding in some cauliflower. 🙂 Thank you for the great recipe.
I would make our favorite breakfast casserole, which includes, shredded hash browns, sausage, Egglands Best
and onions and mushrooms, topped with cheese.
I’ll make my favorite onion corn quiche.
I would make a bacon, jalapeno deviled egg recipe.
I would make a delicious batch of French Lasagna, Sunday breakfast favorite at our house!
I would make a bacon, scallion, and asiago cheese omelet!
I’ll make a broccoli and cheddar quiche!
I would make Deviled Eggs
Oh I would love to make our garden omelets! We love using things we pick from our garden in the summer!
French Toast
I will make quiche if I win this one.
I want to make a sausage mushroom quiche!!!
I am going to make my delicious and healthy apple crunch cake!
I plan on making cheddar cheese & spinach omelets for my family!
I am going to make my Bacon and tomato quiches.
I would make an extra cheesy veggie omelette for my family!
I like to make egg cups with some hamburger and broccoli, they are great for an on the go breakfast and you can freeze them.
I will make my delicious deviled eggs. Always a big hit!
I actually don’t like eggs unless they’re baked into something. Everyone else in my house loves’em, they eat omelettes all the time. If it was up to me I would used Eggland’s Best Eggs to bake a chocolate cake!
I would love to make a chocolate cake with seven minute frosting!
i want to make a steak and egg hash
I would make deviled eggs topped with bacon.
I would make poached eggs. It’s the #1 choice for breakfast here in my house.
I would make a ham and cheese omelet.
My mother used to make us an egg pie. I would like to bake one with scrambled egg, kale, cheese and/or potatoes.
I am a baker by heart.. cookies, cakes, pies, brownies.. I would be thrilled to win this!!!
I would make a spanish omelette.
I like to make egg salad with my Eggland’s Best eggs.
I would make french toast!
I would make an omelet or a broccoli and cheese quiche.
Either way, yum!!! 🙂
thanks!
I would make french toast
I would make my favorite spinach, onion, and bacon quiche!
I would make a strawberry cheesecake.
I love cookies and so does my family.. So I will likely make chocolate chip cookies with walnuts. I love Eggland’s Best eggs anyway for the taste and all the nutritional values it offers over regular store eggs. My sister told me about the taste of these eggs years ago and there is a huge difference.
I would make an omelette recipe, using plenty of cheeses. Thanks
I might make a Southwest Omelet
I would make quiche yummy
I would make deviled eggs.
I would make stuffed mushroom caps with Swiss cheese and artichoke.
I would make a roasted mushroom and feta quiche.
I will be making a mushroom and cheese omelette.
thank you
I would make Creamy Lemon Blueberry Squares.
I would make a fluffy omelet topped with crawfish etouffee.
My little family loves it when I make French Toast on the weekends!
This looks delicious! I would make a quiche lorraine.
Thank you!
I’d make a quiche
I would make a spinach and feta omelette.
I would make Quiche Lorraine.
I will make a ham, egg and cheese scramble.
I would make a ham and cheese omelet.
I would make a sausage and egg casserole.
I will use them to bake a chocolate cake.
Thank you for the chance to win this!
I’d make Bacon and Egg Hash.
I would make kale artichoke egg casserole.
I want to make a vanilla pudding homemade from scratch with the freshest eggs, Eggland’s, and fresh scraped vanilla bean and the best milk! So good!
I would make a scrambled egg and bacon biscuit!
I would make a killer egg salad!
i would love to make omelet
I would make omelet
I’ll make a cobb salad with hard boiled eggs.
I will make a veggie fritatta